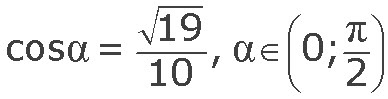Условия всех задач из категории B7

Историческая справка и теоретические сведения

Действия со степенями:

aⁿ · a^m = a^n+m;
aⁿ : a^m = a^n-m;
(aⁿ)^m = a^n·m;
(ab)^m = a^m · b^m.

Логарифмом числа b (b > 0) по основанию a (a > 0, a ≠ 1) называется показатель степени, в которую надо возвести основание a, чтобы получить число b.

log_ab = x `hArr` a^x = b

Основное логарифмическое тождество:

a^log_ab = b (a > 0, a ≠ 1, b > 0)

Основные свойства логарифмов (a > 0, a ≠ 1, b > 0, c > 0):

a) log_aa = 1;

b) log_a1 = 0;

c) log_a(bc) = log_ab + log_ac;

d) log_a(b/c) = log_ab - log_ac;

e) log_ab^p = p · log_ab.

Методические указания

Для успешного решения задач из данной категории вы должны:

уметь выполнять вычисления и проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
знать определения тригонометрических функций, их свойства, табличные значения и знаки по четвертям в тригонометрическом круге;
владеть общими сведениями о степенях и их свойствах;
уметь находить значения корня натуральной степени, степени с рациональным показателем, логарифма;
уметь вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
знать определение логарифма, его свойства и основное логарифмическое тождество.