Условия всех задач из категории C4

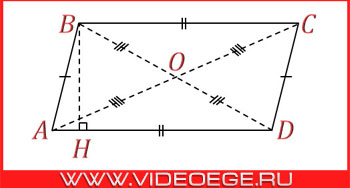Параллелограмм - четырехугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.

ABCD - параллелограмм;

AB || CD,   AD || BC;

AC, BD - диагонали;

BH - высота.

Свойства параллелограмма:

• противоположные стороны равны (AB = CD, AD = BC);

• противоположные углы равны (∠A = ∠C, ∠B = ∠D);

• диагонали точкой пересечения делятся пополам (AO = OC, OD = OB);

• биссектриса отсекает от параллелограмма равнобедренный треугольник;

• сумма всех внутренних углов равна 360°.

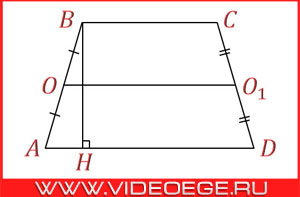Трапеция - четырехугольник, у которого только одна пара противолежащих сторон параллельна.

ABCD - трапеция (BC || AD);

BC, AD - основания;

AB, CD - боковые ребра;

BH - высота;

OO₁ - средняя линия.

Площадь трапеции вычисляется по формуле:

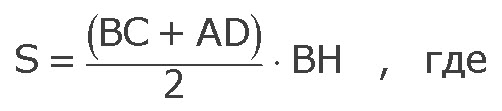
BC, AD - основания трапеции;

BH - высота трапеции.

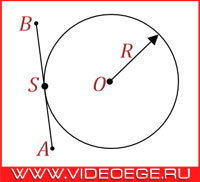
Окружность - геометрическое место точек плоскости, равноудаленных от заданной точки называемой центром, на заданное ненулевое расстояние, называемое ее радиусом.

O - центр окружности;

R - радиус окружности.

Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

AB - касательная к окружности в точке S.

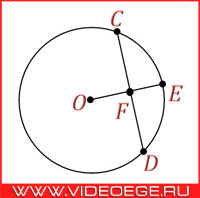
Хорда - отрезок прямой линии, соединяющей две точки окружности.

O - центр заданной окружности;

CD - хорда.

Фундаментальное свойство хорды:

радиус, перпендикулярный к хорде, делит эту хорду пополам.

OF ⊥ CD     `=>`     CF = FD = ½CD

Для успешного решения задач из данной категории вы должны:

1. знать определения геометрических тел и их свойства;

2. уметь проводить дополнительные построения;

3. уметь решать задачи на нахождение геометрических величин (длин, углов, площадей).

Дано:
в параллелограмме ABCD биссектрисы углов при стороне AD делят сторону BC точками M и N так, что BM : MN = 1 : 5.

Вопрос:
найдите BC, если AB = 3.

Дано:
площадь трапеции ABCD равна 90. Диагонали пересекаются в точке O, отрезки, соединяющие середину P основания AD с вершинами B и C, пересекаются с диагоналями трапеции в точках M и N.

Вопрос:
найдите площадь четырехугольника OMPN, если одно из оснований трапеции вдвое больше другого.

Дано:
с центром в точке O₁, располагаемой на биссектрисе угла, равного 60°, проведена окружность радиуса 4.

Вопрос:
найдите радиус окружности, вписанной в данный угол и касающейся данной окружности внешним образом, если известно, что расстояние от точки O₁ до вершины угла равно 10.

Дано:
в окружности, радиус которой равен 5, проведена хорда AB = 8. Точка C лежит на хорде AB так, что AC : BC = 1 : 2.

Вопрос:
найдите радиус окружности, касающейся данной окружности и касающейся хорды AB в точке C.