Условия всех задач из категории B6
Историческая справка и теоретические сведения
 Треугольник - простейшая плоская фигура: три вершины и три стороны. Но с древнейших времен и до наших дней математики занимаются изучением треугольника. За это время было сделано много важных открытий и даже создана новая наука - тигонометрия.
Треугольник - простейшая плоская фигура: три вершины и три стороны. Но с древнейших времен и до наших дней математики занимаются изучением треугольника. За это время было сделано много важных открытий и даже создана новая наука - тигонометрия.
Крупнейший древнегреческий историк Геродот (V век до нашей эры) оставил описание того, как египтяне после каждого разлива Нила заново размечали плодородные участки его берегов, с которых ушла вода. С этого и началась геометрия - "землемерие" (от греческого "гео" - "земля" и "метрео" - "измеряю"). Древние землемеры выполняли геометрические построения, измеряли длины и площади. Астрологи рассчитывали расположение небесных светил - все это требовало весьма обширных познаний о свойствах плоских и пространственных фигур, и в первую очередь о треугольнике.
Изображение треугольников и задачи на треугольники встречаются в египетских папирусах, которым более 4000 лет, в старинных индийских книгах и других древних документах. Уже тогда была известна теорема, получившая впоследствии название теоремы Пифагора, которая применялась для построения прямых углов на местности с помощью веревочного треугольника со сторонами 3, 4, 5 (египетский треугольник).
Через 2000 лет в древней Греции учение о треугольнике достигает высокого уровня. Известны такие древнегреческие ученые, как Архимед, Пифагор, Фалес. Учение о треугольнике развивалось в ионийской школе, основанной в VII веке до нашей эры Фалесом, затем в школе Пифагора. Древние греки решили упорядочить накопленные сведения о треугольнике и написали много трудов. Наиболее совершенной оказалась работа Евклида "Начала" (365-300 до н. э.).
Треугольник - многоугольник с тремя сторонами.
Теорема I: сумма углов треугольника равна 180°.
 Прямоугольный треугольник - это треугольник, в котором один угол прямой (то есть составляет 90°).
Прямоугольный треугольник - это треугольник, в котором один угол прямой (то есть составляет 90°).
∆ABC - прямоугольный (∠ACB = 90°);
AC, BC - катеты;
AB - гипотенуза.
Теорема Пифагора: в прямоугольним треугольнике квадрат гипотенузы равен сумме квадратов катетов.
a2 + b2 = c2, где
a, b - катеты;
c - гипотенуза.
 Равнобедренный треугольник - это треугольник, в котором две стороны равны между собой.
Равнобедренный треугольник - это треугольник, в котором две стороны равны между собой.
Высота треугольника - перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Биссектриса угла - луч с началом в вершине угла, делящий угол на два равных угла.
Медиана треугольника - отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны, а также прямая, содержащая этот отрезок.
Свойство медианы:
медиана треугольника делит его на две равновеликие части.
Свойства равнобедренного треугольника:
а) углы при основании равны (∠A = ∠C);
б) биссектриса, медиана, высота и срединный перпендикуляр, проведенные к основанию, совпадают между собой.
Методические указания
Для успешного решения задач из данной категории вы должны:
уметь выполнять арифметические действия без использования калькулятора;
знать определение треугольника и его свойства;
знать теорему Пифагора и теорему о сумме углов в треугольнике;
знать определения тригонометрических функций, их свойства и табличные значения;
уметь находить неизвестные элементы геометрических фигур по известным значениям тригонометрических функций.
Задача №1
Дано:
в треугольнике ABC отрезок AD – биссектриса, угол C равен 105°, угол CAD равен 7°.

Вопрос:
найдите угол B. Ответ дайте в градусах.
Задача №2
Дано:
в треугольнике ABC угол C равен 90°, угол A равен 30°, AB = `sqrt(3).`
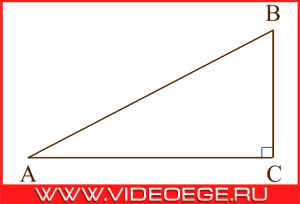
Вопрос:
найдите AC.
Задача №3
Дано:
в треугольнике ABC AC = BC = 4, sin∠B = `sqrt(19)/10`.
Вопрос:
найдите AB.
Задача №4
Дано:
в треугольнике ABC AB = BC, AC = 5, cos∠C = 0.8.
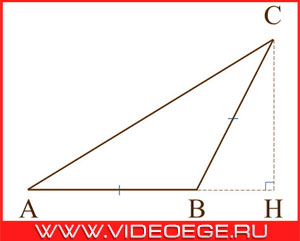
Вопрос:
найдите высоту CH.