Условия всех задач из категории B9
Историческая справка и теоретические сведения
Стереометрия развивалась из наблюдений и решений вопросов, которые возникали в процессе практической деятельности человека. Несомненно, что уже первобытный человек, сменив кочевье на оседлую жизнь, занявшись земледелием, делал попытки оценивать, хотя бы в самых грубых чертах, размер собранного им урожая по массам хлеба, сложенного в кучи, копны или скирды. Строитель даже самых древних примитивных построек должен был как-то учитывать материал, которым он располагал, и уметь подсчитать, сколько материала потребуется для возведения той или иной постройки. Каменотесное дело у древних египтян и халдеев требовало знакомства с метрическими свойствами хотя бы простейших геометрических тел: куба, параллелепипеда, призмы, цилиндра и т.д. Потребности земледелия, мореплавания, ориентировки во времени толкали людей к астрономическим наблюдениям, а последние – к изучению свойств сферы и ее частей, а следовательно, и законов взаимного расположения плоскостей и линий в пространстве.
 В период экономического и культурного расцвета Древней Греции и ее колоний геометрия достигла высокого теоретического развития. Из числа выдающихся геометров Греции вопросами стереометрии интересовались Анаксагор, Демокрит, Гиппократ (V в. до н. э.). Гиппократ является в числе первых, занимавшихся решением знаменитой задачи древности – делийской задачи об удвоении куба. В школе Платона проблемы стереометрии значительно продвинулись. Один из представителей школы Платона Теетет рассмотрел восьмигранник и двадцатигранник и дал впервые теорию некоторых свойств пяти правильных многогранников. Ученик Платона Менехме впервые дал некоторую теорию конических сечений. Величайшая заслуга Евклида состоит в том, что он собрал, обработал и привел в стройную систему дошедший до него материал. Из 13 книг его «Начал» стереометрии отведены XI-XIII книги. Собранные Евклидом сведения о стереометрии дополнил, углубил и расширил величайший математик древности Архимед. Он дал тринадцать полуправильных тел, каждое из которых ограничено правильными многоугольниками, но не одного и того же рода, и вычислил объемы тел вращения. Благодаря трудам Архимеда стереометрия достигла своего кульминационного пункта, и элементарная геометрия в современном ее понимании была окончательно установлена.
В период экономического и культурного расцвета Древней Греции и ее колоний геометрия достигла высокого теоретического развития. Из числа выдающихся геометров Греции вопросами стереометрии интересовались Анаксагор, Демокрит, Гиппократ (V в. до н. э.). Гиппократ является в числе первых, занимавшихся решением знаменитой задачи древности – делийской задачи об удвоении куба. В школе Платона проблемы стереометрии значительно продвинулись. Один из представителей школы Платона Теетет рассмотрел восьмигранник и двадцатигранник и дал впервые теорию некоторых свойств пяти правильных многогранников. Ученик Платона Менехме впервые дал некоторую теорию конических сечений. Величайшая заслуга Евклида состоит в том, что он собрал, обработал и привел в стройную систему дошедший до него материал. Из 13 книг его «Начал» стереометрии отведены XI-XIII книги. Собранные Евклидом сведения о стереометрии дополнил, углубил и расширил величайший математик древности Архимед. Он дал тринадцать полуправильных тел, каждое из которых ограничено правильными многоугольниками, но не одного и того же рода, и вычислил объемы тел вращения. Благодаря трудам Архимеда стереометрия достигла своего кульминационного пункта, и элементарная геометрия в современном ее понимании была окончательно установлена.
После падения Греции наблюдается длительный застой в развитии математики и стереометрии в частности, длившийся тысячу лет. Для развития стереометрии в новое время многое было сделано Кеплером. В своей «Новой стереометрии» - «стереометрии бочек» - он впервые употребил в геометрии бесконечно-малую величину. Открытие Ньютоном и Лейбницем интегрального исчисления окончательно разрешило проблему квадратуры и кубатуры.
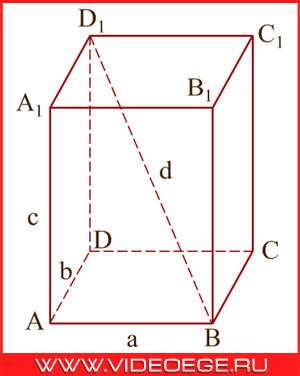 Прямоугольный параллелепипед - это объемная фигура, у которой шесть граней, и каждая из них является прямоугольником.
Прямоугольный параллелепипед - это объемная фигура, у которой шесть граней, и каждая из них является прямоугольником.
ABCDA1B1C1D1 – прямоугольный параллелепипед;
A, B, C, D, A1, B1, C1, D1 – вершины;
AB, BC, CD, AD, AA1, BB1,
CC1, DD1, A1B1, B1C1, C1D1, A1D1 – ребра;
ABB1A1, BCC1B1, CDD1C1, ADD1A1 – боковые грани;
ABCD, A1B1C1D1 – основания;
BD1 – диагональ;
a – длина прямоугольного параллелепипеда;
b – толщина прямоугольного параллелепипеда;
c – высота прямоугольного параллелепипеда.
Объем прямоугольного параллелепипеда:
V = a · b · c
Диагональ (d) прямоугольного параллелепипеда связана с его ребрами соотношением:
d2 = a2 + b2 + c2
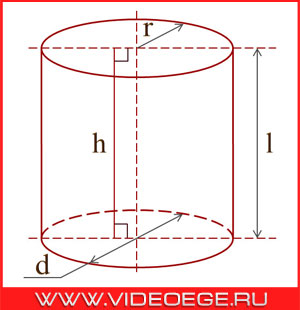 Цилиндр - геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее.
Цилиндр - геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее.
В большинстве случаев под цилиндром подразумевается круговой цилиндр, у которого направляющая – окружность и основания перпендикулярны образующей.
r – радиус цилиндра;
l – образующая цилиндра;
h – высота цилиндра.
Примечание: в прямом круговом цилиндре длина образующей равна длине высоты.
Площадь боковой поверхности рассчитывается по формуле:
Sбок = 2π · r · h, где
π – перманентная величина (≈3.1415);
r – радиус основания цилиндра;
h – высота цилиндра.
Диаметр цилиндра – хорда окружности, проходящая через центр этой окружности.
Диаметр равен двум радиусам:
d = 2 · r
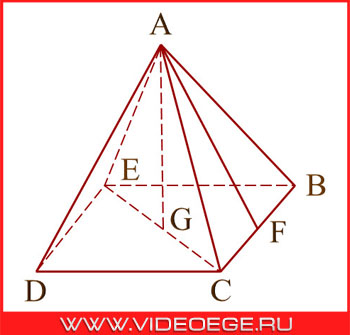 Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.
Правильная пирамида – пирамида, в основании которой лежит правильный многоугольник, а вершина проецируется в центр основания.
A – вершина пирамиды;
AB, AC, AD, AE – ребра пирамиды;
ADE, ACD, ABC, ABE – боковые грани пирамиды;
BCDE – основание пирамиды;
AG – высота пирамиды;
AF – апофема пирамиды;
AEC – диагональное сечение.
Одно из свойств правильной пирамиды:
боковые ребра правильной пирамиды равны.
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания и апофемы.
Sбок = ½ · P · a, где
Sбок - площадь боковой поверхности;
P - периметр основания;
a - апофема.
Методические указания
Для успешного решения задач из данной категории вы должны:
знать определения геометрических тел и их свойства;
уметь выполнять действия с геометрическими фигурами, координатами и векторами;
уметь решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов);
знать формулы расчета площадей и объемов геометричеких тел.
Задача №1
Дано:
в правильной четырехугольной пирамиде SABCD точка O – центр основания, S – вершина, SO = 54, AC = 144.
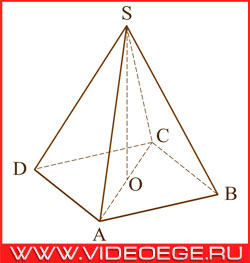
Вопрос:
найдите боковое ребро SB.
Задача №2
Дано:
в правильной треугольной пирамиде SABC K – середина ребра BC, S – вершина. Известно, что AB = 6, а SK = 7.
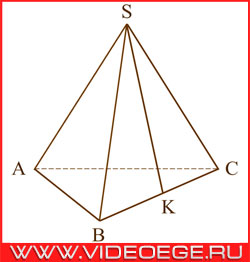
Вопрос:
найдите площадь боковой поверхности.
Задача №3
Дано:
площадь боковой поверхности цилиндра равна 12π, а высота равна 6.
Вопрос:
найдите диаметр основания.
Задача №4
Дано:
в прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BD1 = `sqrt(29)`, BB1 = 3, A1D1 = 4.
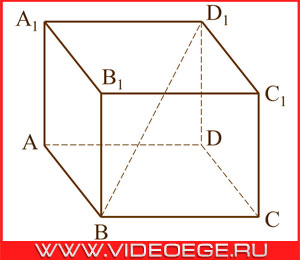
Вопрос:
найдите длину ребра AB.