Условия всех задач из категории B3
Историческая справка и теоретические сведения
Треугольник - многоугольник с тремя сторонами.
 Треугольник называется прямоугольным, если один из его углов равен 90°.
Треугольник называется прямоугольным, если один из его углов равен 90°.
Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
c2 = a2 + b2, где
a, b - катеты прямоугольного треугольника;
c - гипотенуза прямоугольного треугольника.
Площадь прямоугольного треугольника равна половине произведения его катетов:
SABC = ½ · AC · BC = ½ · a · b, где
SABC - площадь прямоугольного треугольника;
a, b - катеты прямоугольного треугольника.
Площадь произвольного треугольника равна половине произведения длины его стороны на высоту, проведенную к этой стороне:
S = ½ · a · h, где
S - площадь произвольного треугольника;
a - сторона треугольника;
h - высота треугольника, проведенная к стороне a.
Параллелограмм - это четырехугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.
 Прямоугольник - параллелограмм, у которого все углы прямые.
Прямоугольник - параллелограмм, у которого все углы прямые.
ABCD - прямоугольник, так как:
∠A = ∠B = ∠C = ∠D = 90°;
AB || CD, AD || BC.
Площадь прямоугольника равна произведению его смежных сторон:
SABCD = AB · AD = a · b, где
SABCD - площадь прямоугольника ABCD;
a, b - смежные стороны прямоугольника.
 Трапеция - четырехугольник, у которого только одна пара противолежащих сторон параллельна.
Трапеция - четырехугольник, у которого только одна пара противолежащих сторон параллельна.
Площадь трапеции равна произведению полусуммы оснований на высоту.
S = ½ · (a + b) · h, где
S - площадь трапеции;
a - длина верхнего основания трапеции;
b - длина нижнего основания трапеции;
h - длина высоты трапеции.

Ромб - четырехугольник, у которого все стороны равны.
ABCD - ромб, так как AB = BC = CD = AD.
AC, BD - диагонали ромба, причем AC ⊥ BD.
Площадь ромба равна половине произведения диагоналей:
SABCD = ½ · AC · BD, где
SABCD - площадь ромба ABCD;
AC, BD - длины диагоналей ромба.
Методические указания
Для успешного решения задач из данной категории вы должны:
знать определения основных геометрических фигур и их свойства;
уметь работать с координатной плоскостью;
уметь находить длины сторон фигур по рисунку и по координатам точек;
знать формулы расчета площадей основных геометрических фигур и теорему Пифагора;
уметь находить площадь фигуры методом разбиения ее на более простые фигуры;
помнить правило: если фигуру разбить на несколько частей, то сумма площадей этих частей равна площади всей фигуры.
Задача №1
Дано:
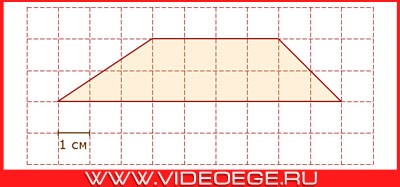
Вопрос:
найдите площадь трапеции, изображенной на клетчатой бумаге, с размером клетки 1 см х 1 см. Ответ дайте в квадратных сантиметрах.
Задача №2
Дано:
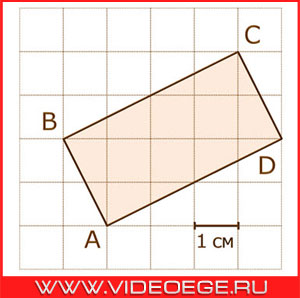
размер каждой клетки 1 см х 1 см.
Вопрос:
найдите площадь прямоугольника ABCD. Ответ дайте в квадратных сантиметрах.
Задача №3
Дано:

вершины параллелограмма имеют координаты (1;7), (9;2), (9;4), (1;9).
Вопрос:
найдите площадь параллелограмма.
Задача №4
Дано:
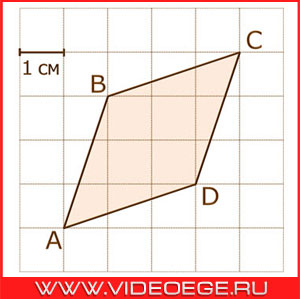
размер каждой клетки 1 см х 1 см.
Вопрос:
найдите площадь ромба ABCD. Ответ дайте в квадратных сантиметрах.