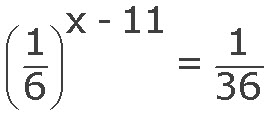Условия всех задач из категории B5
Историческая справка и теоретические сведения
В те далекие времена, когда мудрецы впервые стали задумываться о равенствах содержащих неизвестные величины, наверное, еще не было ни монет, ни кошельков. Но зато были кучи, а также горшки, корзины, которые прекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов. "Ищется куча, которая вместе с двумя третями ее, половиной и одной седьмой составляет 37...", - поучал во II тысячелетии до новой эры египетский писец Ахмес. В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы довольно успешно справлялись с такими задачами.
Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: "Смотри!", "Делай так!", "Ты правильно нашел". В этом смысле исключением является "Арифметика" греческого математика Диофанта Александрийского (III в.) – собрание задач на составление уравнений с систематическим изложением их решений.
Однако первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда бен Мусы аль-Хорезми. Слово "аль-джебр" из арабского названия этого трактата – "Китаб аль-джебер валь-мукабала" ("Книга о восстановлении и противопоставлении") – со временем превратилось в хорошо знакомое всем слово "алгебра", а само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.
Уравнение - это равенство, в котором содержится неизвестная величина (переменная).
Основные виды простейших уравнений:
линейные;
квадратные;
дробно-рациональные;
иррациональные;
показательные;
логарифмические;
тригонометрические.
Линейные уравнения - это уравнения вида ax = b, где неизвестным является x, а буквы a и b обозначают заданные числа.
Если a = 0, то либо уравнение не имеет корней, либо x может быть любым числом.
При a ≠ 0, корень уравнения находят по формуле: x = b : a.
Квадратные уравнения - это уравнения вида ax2 + bx + c = 0, где a ≠ 0.
Основная формула для решения квадратного уравнения:
Иррациональным уравнением относительно переменной x называется уравнение, содержащее эту искомую величину под знаком радикала.
Решение иррационального уравнения следует искать в области допустимых значений данной переменной.
ОДЗ (область допустимых значений) - значения неизвестной, при которых алгебраическое выражение имеет смысл.
Простейшее показательное уравнение - это уравнение вида:
ax = b, где a > 0, a ≠ 1.
При b > 0 это уравнение имеет единственный корень.
При b ≤ 0 это уравнение корней не имеет.
Теорема I: уравнение af(x) = ag(x) (a > 0, a ≠ 1) равносильно уравнению f(x) = g(x).
Логарифмом числа b (b > 0) по основанию a (a > 0, a ≠ 1) называется показатель степени, в которую надо возвести основание a, чтобы получить число b.
Обозначение: logab.
Из определения: logab = x `hArr` ax = b.
Уравнение вида logaf(x) = b (a > 0, a ≠ 1) обычно решается по определению логарифма и необходимо выполнение условия:
f(x) ≥ 0.
Тригонометрическое уравнение - это уравнение, содержащее неизвестное под знаком тригонометрической функции.
Решение любого тригонометрического уравнения сводится к решению одного из трех видов простейших тригонометрических уравнений: sinx = a, cosx = a или tgx = a.
Методические указания
Для успешного решения задач из данной категории вы должны:
знать определение модуля и его свойства;
уметь находить область допустимых значений;
владеть общими сведениями о степенях и их свойствах;
уметь решать квадратные, рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения, неравенства и их системы;
знать основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных;
уметь использовать графики функций при решении уравнений.
