Условия всех задач из категории B8

Функция - одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира. Идея функциональной зависимости восходит к древности. Ее содержание обнаруживается уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами, в первых формулах для нахождения площади и объема тех или иных фигур. Так, вавилонские ученые (4-5тыс.лет назад) пусть несознательно, установили, что площадь круга является функцией от его радиуса посредством нахождения грубо приближенной формулы: S = 3r².

Примерами табличного задания функции могут служить астрономические таблицы вавилонян, древних греков и индийцев, а примерами словесного задания функции - теорема о постоянстве отношения площадей круга и квадрата на его диаметре или античные определения конических сечений, причем сами эти кривые выступали в качестве геометрических образов соответствующей зависимости.

Путь к появлению понятия функции заложили в 17 веке французские ученые Франсуа Виет и Рене Декарт; они разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание. Введено было единое обозначение: неизвестных - последними буквами латинского алфавита x, y, z, ... - известных - начальными буквами того же алфавита - a, b, c, ... и т.д. Тем самым появилась возможность записывать общие формулы.

Кроме того, у Декарта и Ферма в геометрических работах появляется отчетливое представление переменной величины и прямоугольной системы координат. В своей «Геометрии» в 1637 году Декарт дает понятие функции, как изменение ординаты точки в зависимости от изменения ее абсциссы; он систематически рассматривал лишь те кривые, которые можно точно представить с помощью уравнений, притом преимущественно алгебраических. Постепенно понятие функции стало отождествляться, таким образом, с понятием аналитического выражения - формулы.

В 1671 году Ньютон под функцией стал понимать переменную величину, которая изменяется стечением времени. В «Геометрии» Декарта и работах Ферма, Ньютона и Лейбница понятие функции носило по существу интуитивный характер и было связано либо с геометрическими, либо с механическими представлениями.

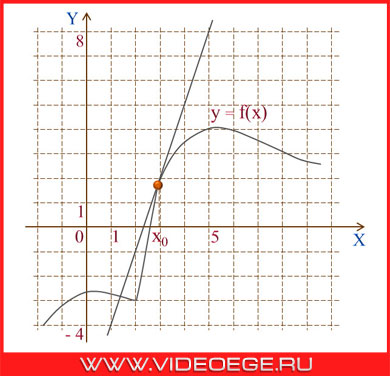График функции - множество точек, у которых абсциссы являются допустимыми значениями аргумента х, а ординаты - соответствующими значениями функции у.

Касательная - прямая линия, имеющая одну общую точку с кривой.

Существование производной функции f в точке x₀ эквивалентно существованию    (невертикальной)   касательной   в   точке (x₀; f(x₀)) графика функции, при этом угловой коэффициент касательной равен f '(x₀). В этом и состоит геометрический смысл производной.

Также  известно,  что  значение  производной  в  точке, то есть f '(x₀), равно тангенсу угла наклона касательной графика функции f(x) в точке с абсциссой x₀ к положительному направлению оси Ox:

f '(x₀) = tgα

Примечание: если рассматривается угол наклона к отрицательному направлению оси Ox, то:

f '(x₀) = - tgα

Тангенсом угла α называется отношение противолежащего катета к прилежащему катету.

Критические точки - внутренние точки области определения функции, в которых ее производная равна нулю или не существует.

Признак максимума функции: если функция f непрерывна в точке x₀, а f '(x₀) > 0 на интервале (a; x₀) и f '(x₀) < 0 на интервале (x₀; b), то точка x₀ является точкой максимума функции.

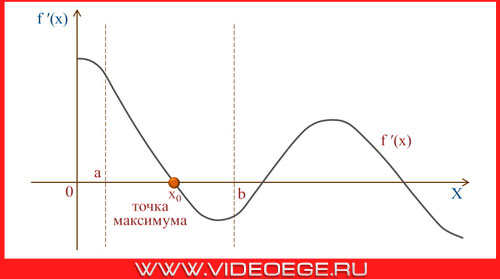
Признак минимума функции: если функция f непрерывна в точке x₀, а f '(x₀) < 0 на интервале (a; x₀) и f '(x₀) > 0 на интервале (x₀; b), то точка x₀ является точкой минимума функции.

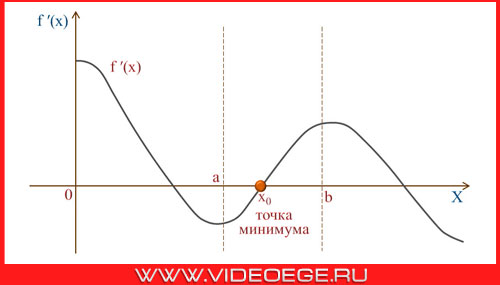
Точки экстремума - точки максимума и минимума.

Промежутки монотонности функции - промежутки, на которых функция возрастает (убывает).

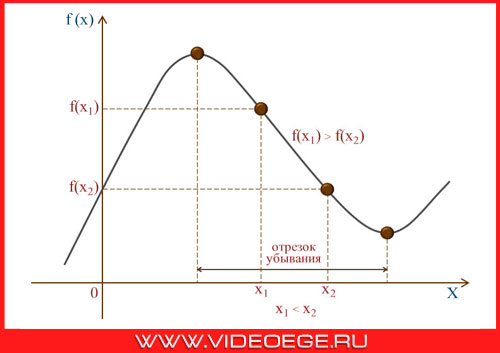
Функция f возрастает на множестве x, если для любых x₁ и x₂ из множества x,  таких,  что x₁ < x₂,  выполняется  неравенство f(x₁) < f(x₂).

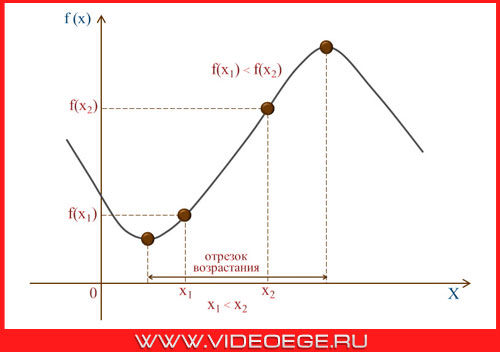
Функция f убывает  на  множестве x,  если  для  любых x₁ и x₂ из  множества x,  таких,  что x₁ < x₂, выполняется  неравенство f(x₁) > f(x₂).

Теорема I (необходимое и достаточное условие возрастания функции):
если дифференцируемая функция y = f(x) возрастает на [a, b], то ее производная неотрицательна на этом отрезке, f '(x) ≥ 0.

Для успешного решения задач из данной категории вы должны:

1. уметь читать график функции и график производной функции;

2. знать геометрический смысл производной;

3. знать определение касательной и уметь находить угловой коэффициент касательной;

4. знать чему равен тангенс угла;

5. уметь находить расстояние между двумя точками;

6. уметь определять промежутки возрастания и убывания функции по графику ее производной;

7. уметь находить точки экстремума, точки максимума и минимума функции на отрезке по графику ее производной;

8. уметь детерминировать по графику функции точки, в которых производная функции равна нулю.

Дано:
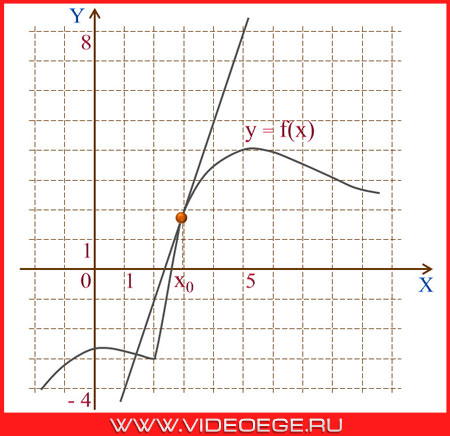
на рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x₀.

Вопрос:
найдите значение производной функции f(x) в точке x₀.  

Дано:
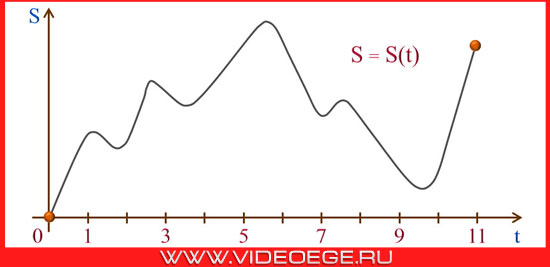
материальная точка M начинает движение из точки A и движется по прямой на протяжении 11 секунд. График показывает, как менялось расстояние от точки A до точки M со временем. На оси абсцисс откладывается время t в секундах, на оси ординат – расстояние s в метрах.

Вопрос:
определите, сколько раз за время движения скорость точки M обращалась в нуль (начало и конец движения не учитывайте).

Дано:
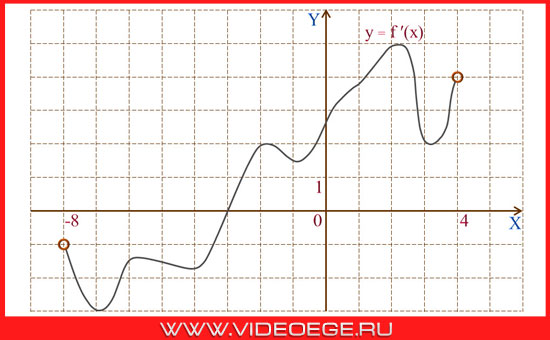
на рисунке изображен график производной функции f(x), определенной на интервале (– 8; 4).

Вопрос:
найдите точку экстремума функции f(x) на отрезке [– 7; 0].

Дано:
на рисунке изображен график функции y = f(x).

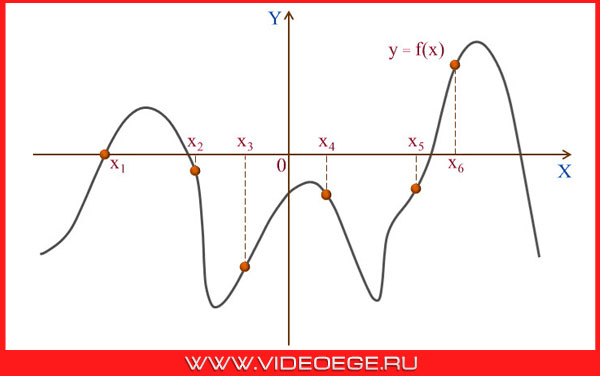
Вопрос:
найдите среди точек x₁, x₂, x₃, x₄, x₅ и x₆ те точки, в которых производная функции f(x) положительна. В ответ запишите количество найденных точек.