Дано:
натуральные числа m и n таковы, что и m³ + n, и m + m³ делится на m² + n².

Вопрос:
найдите m и n.

I. Поскольку числа m и n являются натуральными, то суммы (m³ + n), (m³ + m) и (m² + n²) также являются натуральными числами.

Учитывая, что (m² + n²) является делителем чисел (m³ + n) и (m³ + m) получим:

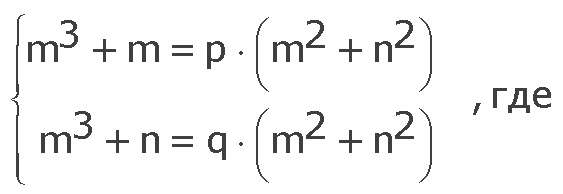
p и q - делители чисел (m³ + m) и (m³ + n) соответственно.

1 вариант: пусть m ≥ n.

Тогда m³ + m ≥ m³ + n, следовательно:

p · (m² + n²) ≥ q · (m² + n²)     / : (m² + n²) ≠ 0

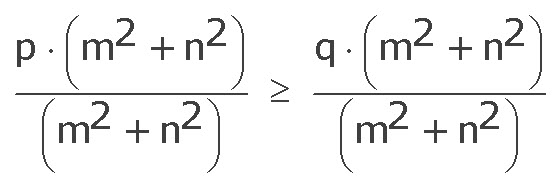
p ≥ q

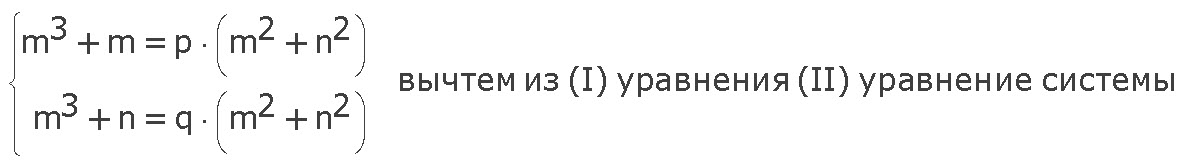
m³ + m - (m³ + n) = p · (m² + n²) - q · (m² + n²)

m³ + m - m³ - n = (p - q) · (m² + n²)

m - n = (p - q) · (m² - n²)

Обозначим за:

• A = m - n;

• B = p - q.

Получим:

A = B · (m² + n²)

Используя формулу (a - b)² = a² - 2ab + b², имеем:

(m - n)² = A² = m² - 2mn + n², откуда:

m² + n² = A² + 2mn

Имеем:

A = B · (A² + 2mn)

A = B · A² + B · 2mn

BA² - A + 2mn · B = 0

это квадратный трехчлен, при условии, что:

B = (p - q) ≠ 0

D = b² - 4ac = (-1)² - 4 · B · 2 · m · n · B = 1 - 8mn · B²

Чтобы уравнение имело вещественные корни, необходимо выполнение условия:

D ≥ 0, то есть:

1 - 8mn · B² ≥ 0

Поскольку m и n - натуральные числа, то

8mn >> 1, следовательно, B должен быть равным 0, то есть:

B = 0

p - q = 0

p = q

Следовательно, сформированное уравнение:

BA² - A + 2mn · B = 0 принимает вид:

0 · A² - A + 2mn · 0 = 0

0 - A + 0 = 0

-A = 0     / · (-1) ≠ 0

(-1) · (-A) = 0 · (-1)

A = 0

Учитывая, что A = m - n, имеем:

m - n = 0

m = n

Уравнение m³ + m = p · (m² + n²) примет вид:

m³ + m = p · (m² + m²)

m(m² + 1) = p · 2m²     / : m ≠ 0

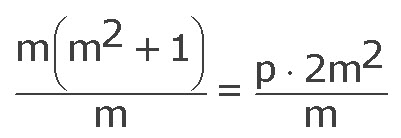
m² + 1 = 2pm

m² - 2pm + 1 = 0     (a = 1, b = -2p, c = 1)

это квадратный трехчлен, относительно m.

D = b² - 4ac = (-2p)² - 4 · 1 · 1 = 4p² - 4 = 4(p² - 1)

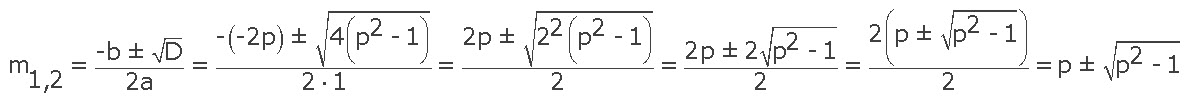
Данный арифметический корень `sqrt(p^2-1)` вернет целочисленное значение только при p = 1, то есть:

m₁ = p = 1

m₂ = p = 1

m₁ = m₂ = 1

Учитывая, что m = n, имеем:

m = n = 1

2 вариант: пусть m < n.

Тогда m³ + m < m³ + n, следовательно:

p · (m² + n²) < q · (m² + n²)     / : (m² + n²) ≠ 0

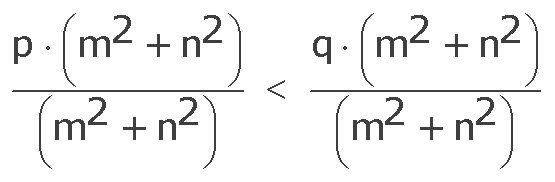
p < q

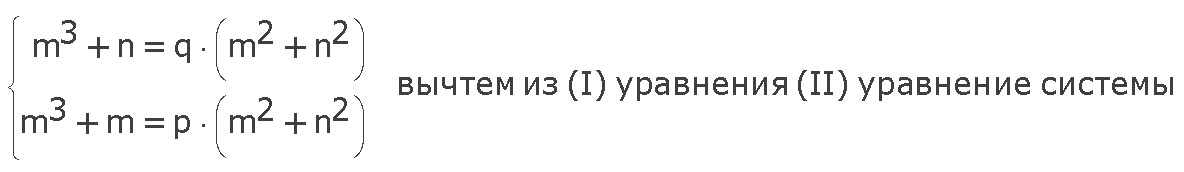
m³ + n - (m³ + m) = q · (m² + n²) - p · (m² + n²)

m³ + n - m³ - m = (q - p) · (m² + n²)  

n - m = (q - p) · (m² + n²)  

Обозначим за:

• C = n - m;

• D = q - p.

Получим:

C = D · (m² + n²)

Используя формулу (a - b)² = a² - 2ab + b², имеем:

(n - m)² = C² = n² - 2nm +m², откуда:

m² + n² = C² + 2nm

Имеем:

C = D · (C + 2nm)

C = D · C² + D · 2nm

DC² - C + 2nm · D = 0     (a = D, b = -1, c = 2nm · D)

D = b² - 4ac = (-1)² - 4 · D · 2 · n · m · D = 1 - 8nm · D²

Чтобы уравнение имело вещественные корни, необходимо, чтобы дискриминант был величиной неотрицательной, то есть:

1 - 8nm · D² ≥ 0

Поскольку m и n - натуральные числа, то

8mn >> 1, следовательно, D должен быть равным 0, то есть:

D = 0

q - p = 0

q = p, но это противоречит условию, что p < q. То есть m не может быть меньше n.